The delta method is a simple trick to find the standard deviation of a transformed random variable.
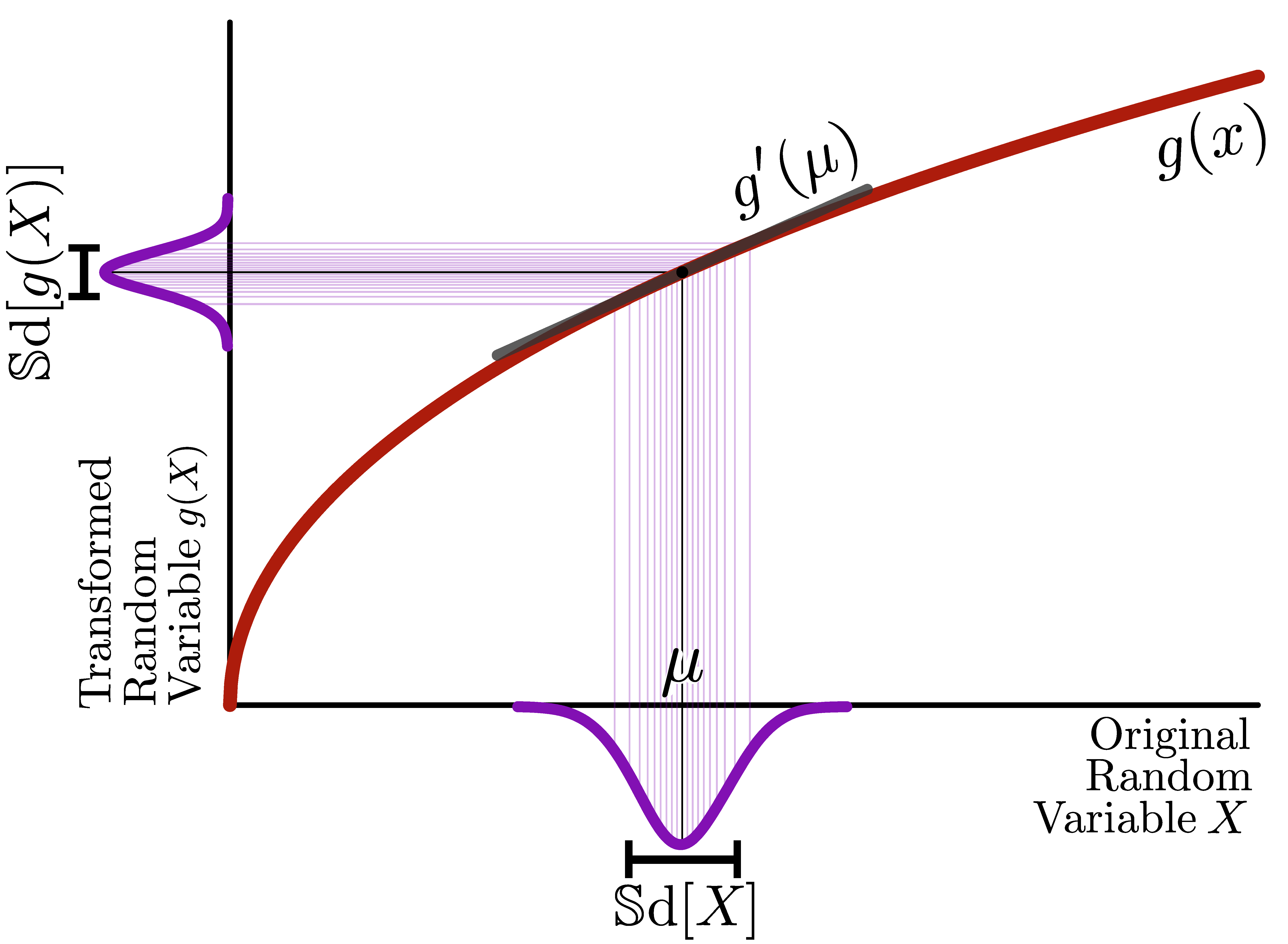
If we apply a differentiable function \(g\) to a random variable \(X\) with mean \(\mu\), the standard deviation of the transformed random variable \(g(X)\) can be approximated by \[ \mathbb{S}\text{d}[g(X)] \approx a\; \mathbb{S}\text{d}[X], \] where \(a = |g'(\mu)|\) is the slope of \(g\) at \(\mu\).
And what about variance stabilizing transformations?
Now consider a set of random variables \(X_1, X_2, \cdots\) whose variance and means are related through some function \(v\), i.e. \(\mathbb{V}\text{ar}[X_i] = v(\mu_i)\), or equivalently \(\mathbb{S}\text{d}[X_i] = \sqrt{v(\mu_i)}\). Then we can find a variance-stabilizing transformation \(g\) by requiring constant standard deviation, \(\mathbb{S}\text{d}[g(X_i)] = \text{const.}\), which using the above approximation becomes \[ g'(\mu) = \frac{\text{const}}{\sqrt{v(\mu)}}, \] and can be solved by integration.
Example
The Gamma-Poisson distribution (also called Negative binomial) with mean \(\mu\) and overdispersion \(\alpha\) implies a quadratic mean-variance relation \[ \mathbb{V}\text{ar}[X] = v(\mu) = \mu + \alpha \mu^2. \] Our goal is to find a function \(g\) for which \[ \mathbb{S}\text{d}[g(X)] \approx \text{const.} \] The delta method approximates the standard deviation of a transformed random variable as \[ \mathbb{S}\text{d}[g(X)] \approx |g'(\mu)|\;\mathbb{S}\text{d}[X]. \] We can require the left side to be constant and solve for \(|g'(\mu)|\): \[\begin{equation} \begin{aligned} |g'(\mu)|\;\mathbb{S}\text{d}[X] &= \text{const.} \\ g'(\mu) &= \frac{\text{const.}}{\mathbb{S}\text{d}[X]} = \frac{\text{const.}}{\sqrt{v(\mu)}} \end{aligned} \end{equation}\]
Given the derivative \(g'\), we can use integration to identify the functional form of our transformation (note that without loss of generality, we can plug in \(1\) for the constant, as the value does not affect the variance stabilization property.) \[\begin{equation} \begin{aligned} g(\mu) &= \int{\frac{1}{\sqrt{v(\mu)}} \text{d}\mu} \\ &= \int{\frac{1}{\sqrt{\mu+\alpha \mu^2}}\text{d}\mu} \\ &= \frac{2}{\sqrt{\alpha}} \operatorname{asinh}\left(\sqrt{\alpha \mu}\right) \\ &= \frac{1}{\sqrt{\alpha}} \operatorname{acosh}\left(2 \alpha \mu +1\right). \end{aligned} \end{equation}\] You can check the integration using Wolfram Alpha.
If there is no overdispersion (\(\alpha = 0\)), the acosh transformation reduces to the well-known square root variance stabilizing transformation for Poisson random variables \[\begin{equation} \lim_{\alpha \to 0} g(\mu) = 2\sqrt{\mu}. \end{equation}\]
Learn more
The original explainer on the delta method was published in Ahlmann-Eltze and Huber (2022). The Modern Statistic for Modern Biology text book also contains a didactic introduction to the delta method (Holmes and Huber 2018). The original method and the name is due to Dorfman (1938) and an interesting article (Ver Hoef 2012) retraces the invention.
