This blog post provides a simplified implementation of the LEMUR method. The full details of the method are described in the Methods and Supplementary information of our paper “Analysis of multi-condition single-cell data with latent embedding multivariate regression”. However, translating the formulas to code can be difficult. On the other hand, our reference implementations–the lemur R package–contains over 3500 lines of code, which can make it equally difficult to identify the relevant pieces.
Here, I will give a stripped-down implementation of LEMUR so that anyone can build on the algorithm!
Multi-condition PCA
LEMUR relates the subspaces occupied by cells from different conditions to each other through multi-condition PCA. This can be implemented with the following three functions.
To learn more about the Grassmann manifolds and where the algorithms for the exponential and logarithmic map come from, take a look at the Grassmann manifold handbook by Bendokat et al.
#' @param p,q two orthonormal matrices of size `N x M` (i.e., `t(p) %*% p == diag(nrow=N)`)
#' that both represent an `M` dimensional subspace in the `N` dimensional gene space.
#'
#' @return the tangent vector to go from point `p` to `q` on the Grassmann manifold
#' represented as an `N x M` dimensional matrix.
grassmann_log <- function(p, q){
n <- nrow(p)
k <- ncol(p)
z <- t(q) %*% p
At <- t(q) - z %*% t(p)
Bt <- lm.fit(z, At)$coefficients
svd <- svd(t(Bt), k, k)
svd$u %*% diag(atan(svd$d), nrow = k) %*% t(svd$v)
}
#' @param x a tangent vector (represented as an `N x M` dimensional matrix.)
#' @param base_point orthonormal matrix of size `N x M`
#'
#' @return the point on the Grassmann manifold reached after going one step
#' in direction `x` from the `base_point`.
grassmann_map <- function(x, base_point){
svd <- svd(x)
base_point %*% svd$v %*% diag(cos(svd$d), nrow = length(svd$d)) %*% t(svd$v) +
svd$u %*% diag(sin(svd$d), nrow = length(svd$d)) %*% t(svd$v)
}The inputs for the multicondition_pca function are the log-normalized counts for each cell, a design matrix, and the number of latent dimensions.
It returns the joint embedding of all cells and the coefficients of the LEMUR model.
#' @param Y is a matrix with features in the rows and observations in the columns.
#' @param design_matrix a matrix with one row per observation which encodes the
#' known covariates.
#'
#' @return a list with the embedding, the base_point, the coefficients for the
#' Grassmann exponential map, and the coefficients for the linear regression.
multicondition_pca <- function(Y, design_matrix, n_embedding = 15){
# Center observations with linear regression
fit <- lm.fit(design_matrix, t(as.matrix(Y)))
Y <- t(residuals(fit))
# Find base point with PCA over all data points
base_point <- irlba::prcomp_irlba(t(Y), n = n_embedding, center = FALSE)$rotation
# Find the subspace for each condition
red_design <- unique(design_matrix)
cond_ids <- vctrs::vec_group_id(design_matrix)
cond_weights <- c(table(cond_ids))
cond_subspaces <- lapply(seq_len(nrow(red_design)), \(cond){
# Fit one PCA for each unique combination of covariates
irlba::prcomp_irlba(t(Y[,cond_ids == cond,drop=FALSE]),
n = n_embedding, center = FALSE)$rotation
})
# Find coefficients of the Grassmann exponential map
log_points <- do.call(cbind, lapply(cond_subspaces, \(subspace){
# Instead of performing the regression directly on the Grassmann manifold
# I will work in the tangent space of the `base_point`
as.vector(grassmann_log(base_point, subspace))
}))
# Finding the coefficients is just weighted linear regression (as we are working in
# the tangent space)
coefficients <- t(lm.wfit(red_design, t(log_points), w = cond_weights)$coefficients)
# Reshape the coefficients into a three-dimensional array
coefficients <- array(coefficients, dim = c(nrow(Y), n_embedding, ncol(design_matrix)))
# Project each cell on the fitted subspace for the corresponding condition.
embedding <- matrix(NA, nrow = n_embedding, ncol = ncol(Y))
for(cond in seq_len(nrow(red_design))){
tang_vec <- matrix(0, nrow = nrow(Y), ncol = n_embedding)
for(k in seq_len(ncol(red_design))){
# The tangent space is a vector space. This means a weighted sum of the tangent
# vectors is still in the tangent space.
tang_vec <- tang_vec + red_design[cond, k] * coefficients[,,k]
}
# The position of the condition-specific subspace is determined by the fitted
# tangent vector
fitted_cond_subspace <- grassmann_map(tang_vec, base_point)
# Projecting onto the subspace is just matrix multiplication because
# `fitted_cond_subspace` is an orthonormal matrix.
embedding[,cond_ids == cond] <- t(fitted_cond_subspace) %*% Y[,cond_ids == cond]
}
# Order the axes of the `embedding` by variance to make the results akin to PCA
# This means we also need to update the `base_point` and `coefficients`
svd_emb <- svd(embedding)
embedding <- t(svd_emb$v) * svd_emb$d
base_point <- base_point %*% svd_emb$u
for(k in seq_len(ncol(design_matrix))){
coefficients[,,k] <- coefficients[,,k] %*% svd_emb$u
}
# Return results
list(embedding = embedding, base_point = base_point,
coefficients = coefficients, linear_coefficients = t(fit$coefficients))
}Validate
To test the functions, I will load some example data and compare the results of multicondition_pca against the lemur package.
set.seed(1)
sce <- muscData::Kang18_8vs8()
# Apply log transformation to variance-stabilize the values
logcounts(sce) <- transformGamPoi::shifted_log_transform(sce)
# Work on highly variable genes (HVGs) to speed up inference
hvg <- order(-MatrixGenerics::rowVars(logcounts(sce)))
sce <- sce[hvg[1:500], ! is.na(sce$cell)]design_matrix <- model.matrix(~ stim, data = colData(sce))
res <- multicondition_pca(logcounts(sce), design_matrix = design_matrix, n_embedding = 8)
lemur_fit <- lemur::lemur(logcounts(sce), design = design_matrix, n_embedding = 8,
test_fraction = 0, verbose = FALSE)I use all.equal to test if the results are close:
all.equal(res$linear_coefficients, lemur_fit$linear_coefficients)
# The coefficients and embedding are equal up to a sign flip
all.equal(abs(res$coefficients), abs(lemur_fit$coefficients), check.attributes = FALSE)
all.equal(abs(res$embedding), abs(lemur_fit$embedding), check.attributes = FALSE)
# The matrices that represent the base_points are not necessarily equal,
# but they always span the same space, which means the Grassmann logarithmic map is zero.
all.equal(grassmann_log(res$base_point, lemur_fit$base_point),
matrix(0, nrow = nrow(sce), ncol = 8), tolerance = 1e-6)## [1] TRUE
## [1] "Mean relative difference: 5.303032e-05"
## [1] "Mean relative difference: 3.020606e-06"
## [1] TRUEAlignment
The multi-condition PCA alignment is a rigid transformation. This is sometimes not flexible enough to ensure that corresponding cells from different conditions end up in the same position. Here, I provide the code to align cells according to predefined groups with an affine transformation.
The align function is useful beyond the LEMUR algorithm. Existing integration tools (e.g., Harmony, optimal transport, or mutual nearest neighbors (MNN)) find one shift per cluster or cell. Instead, the align function finds a single invertible transformation. This has two advantages: (1) it protects against integration artifacts, and (2) it allows to go back from the integrated embedding to the original gene space.
#' Solve penalized regression of |Y - X b|^2 + lambda * |b|^2
ridge_regression <- function(Y, X, ridge_penalty = 0, weights = rep(1, nrow(X))){
ridge_penalty <- diag(ridge_penalty, nrow = ncol(X))
weights_sqrt <- sqrt(weights)
X_extended <- rbind(X * weights_sqrt, sqrt(sum(weights)) * (t(ridge_penalty) %*% ridge_penalty))
Y_extended <- cbind(t(t(Y) * weights_sqrt), matrix(0, nrow = nrow(Y), ncol = ncol(X)))
qr <- qr(X_extended)
t(solve(qr, t(Y_extended)))
}
#' @param embedding matrix of low-dimensional positions for each cell. Each
#' column is one cell.
#' @param design_matrix the design matrix with one row per cell. Same as
#' for `multicondition_pca`.
#' @param groups a vector with one element per cell. This could, for example,
#' be pre-existing cell type annotations.
#' @param ridge_penalty penalty that favors transformations that are close to the
#' identity matrix and thus avoid overfitting.
align <- function(embedding, design_matrix, groups, ridge_penalty = 0.01){
# Get IDs for conditions and groups
cond_ids <- vctrs::vec_group_id(design_matrix)
group_ids <- as.integer(as.factor(groups))
n_emb <- nrow(embedding)
# Find the target position so that cells from the same group overlap
target_pos <- matrix(0, nrow = n_emb, ncol = ncol(embedding))
for(gr in seq_len(max(group_ids))){
# The target position of each cell after the alignment is calculated for each
# group independently:
# 1. Find the mean position per condition (`cond_means`)
cond_means <- do.call(cbind, lapply(seq_len(max(cond_ids)), function(co){
rowMeans2(embedding, cols = group_ids == gr & cond_ids == co)
}))
# 2. Find the center of those means (`mean_center`)
mean_center <- rowMeans(cond_means)
# 3. Shift all cells so that the mean per condition moves to the center
for(co in seq_len(max(cond_ids))){
sel <- group_ids == gr & cond_ids == co
target_pos[,sel] <- embedding[,sel] + (mean_center - cond_means[,co])
}
}
# Find the best affine transformation to move the `embedding` towards
# `target_pos` with ridge regression.
# The Kronecker products (`%x%`) expand the columns / rows for the design
# matrix / embedding so that I can form all combinations.
interact_design_matrix <- (design_matrix %x% matrix(1, ncol = n_emb + 1)) *
(matrix(1, ncol = ncol(design_matrix)) %x% t(rbind(1, embedding)))
# The `Y` is the difference between target_pos and embedding, so that larger penalties
# favor transformations that are more similar to the identity matrix.
alignment_coefs <- ridge_regression(Y = target_pos - embedding, X = interact_design_matrix,
ridge_penalty = ridge_penalty)
# Reshape the results in a 3D array
alignment_coefs <- array(alignment_coefs, dim = c(n_emb, n_emb + 1, ncol(design_matrix)))
# Apply the transformation to the embedding
for(id in unique(cond_ids)){
# The tangent vector is defined as the `vec = I + \sum_k V_::k` to make sure that the
# ridge penalty shrinks the transformation towards no change
tang_vec <- cbind(0, diag(nrow = n_emb))
covars <- design_matrix[which(cond_ids == id)[1], ]
for(k in seq_len(ncol(design_matrix))){
tang_vec <- tang_vec + covars[k] * alignment_coefs[,,k]
}
embedding[,cond_ids == id] <- tang_vec %*% rbind(1, embedding[,cond_ids == id])
}
# Return results
list(alignment_coefs = alignment_coefs, embedding = embedding)
}Validate
I use the existing cell type annotations to align the conditions. I compare the result of align against lemur::align_by_grouping.
# The `cell` column contains the pre-existing cell type annotations
table(colData(sce)$cell)##
## B cells CD14+ Monocytes CD4 T cells CD8 T cells
## 2880 6447 12033 2634
## Dendritic cells FCGR3A+ Monocytes Megakaryocytes NK cells
## 472 1914 346 2330# Call alignment functions
al_res <- align(res$embedding, design = design_matrix, groups = sce$cell, ridge_penalty = 0.01)
lemur_fit <- lemur::align_by_grouping(lemur_fit, grouping = sce$cell, ridge_penalty = 0.01,
design = design_matrix, verbose = FALSE)
# The results are equal up to a sign flip
all.equal(abs(al_res$alignment_coefs), abs(lemur_fit$alignment_coefficients))## [1] "Mean relative difference: 7.966932e-06"Lastly, I plot a UMAP of the two embeddings to show how similar the results are.
library(tidyverse, warn.conflicts = FALSE)
library(patchwork)
# Despite setting the seed, the results are not 100% identical due to
# numerical instability.
set.seed(1)
umap_manual <- uwot::umap(t(al_res$embedding))
set.seed(1)
umap_lemur <- uwot::umap(t(lemur_fit$embedding))
plot_data <- function(color_by){
as_tibble(colData(sce)) |>
mutate(umap_manual, umap_lemur) |>
pivot_longer(starts_with("umap"), names_to = "method", values_to = "umap") |>
sample_frac(size = 1) |>
ggplot(aes(x = umap[,1], y = umap[,2])) +
geom_point(aes(color = {{color_by}}), size = 0.3, stroke = 0) +
coord_fixed() +
guides(color = guide_legend(override.aes = list(size = 2))) +
facet_wrap(vars(method)) +
theme_void()
}
plot_data(color_by = cell) / plot_data(color_by = stim)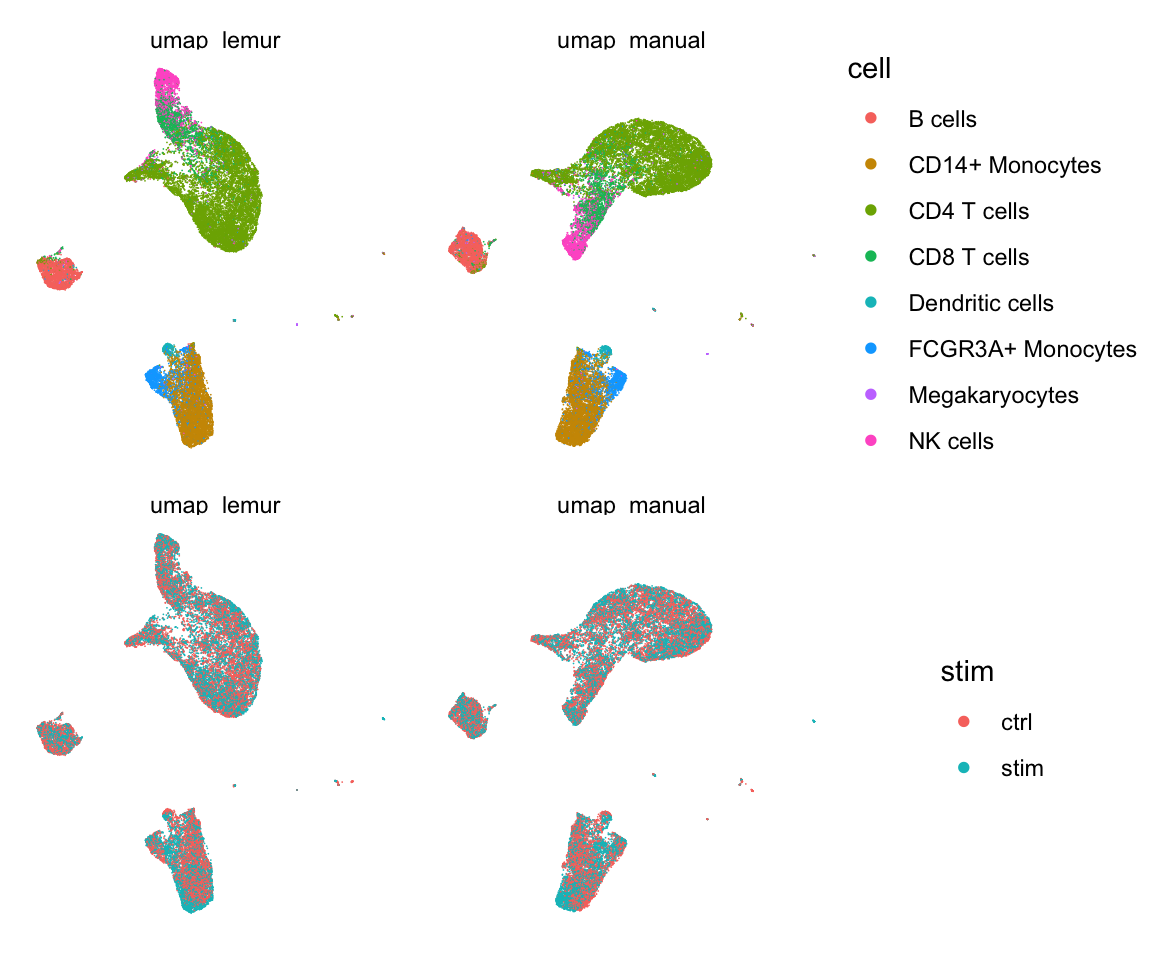
The full code is also available as a gist.
